Riemann’s zeta function and the prime series display a biotic pattern of diversification, novelty, and complexity

Louis H. Kauffman and Hector Sabelli

University of Illinois at Chicago and Chicago Center for Creative Development, Chicago, IL

kauffman@uic.edu

Here we investigate the processes of accumulation and rotation in the generation of novelty by examining series generated by the accumulation of primes and approximations to the primes via progressive divisibility selections, and series generated by Riemann’s equation. Riemann’s zeta function is a re-encoding of the structure of the prime numbers. These studies indicate that the generation of primes is a fundamental example of causal creativity generated by biotic processes.

1 Introduction

The generation of primes epitomizes the causal creation of novelty. The prime series, in fact, shows a biotic pattern [Sabelli, 2007]. Bios is a causally-generated pattern characterized by diversification, novelty and complexity [Kauffman and Sabelli, 1998; Kauffman, and Sabelli, 2003; Sabelli, 2005]. The main tool for measuring bios is the plotting and quantification of isometries compared to those for shuffled versions of the series [Sabelli and Kauffman, 1999; Sabelli et al, 2005].

Not only the prime number series displays a biotic pattern, but also the process that generates the prime series appears to be biotic insofar as it involves accumulation and periodicity or rotation, which are the two components of recursions that generate biotic patterns, such as the process equation [Kauffmann and Sabelli, 1998] and the Schrödinger equation [Sabelli and Kovacevic, 2006]. Accumulation and rotation correspond to fundamental and universal components of natural processes; thus radiation involves the conservation and propagation of energy and the helical pattern of electrical and magnetic polarity.

The number series also involve accumulation and rotation like features. Numbers are generated by the fundamental process of accumulation, the addition of one. Given an integer N, we always have a new integer N+1 which is different from all the previous integers. This process alone is deterministic and generates novelty, namely the primes. Furthermore every integer has a unique factorization as a product of primes, so the novelty generated by this process is reflected by every integer generated by the addition process. Each prime is the originator of the infinite set of its multiples. The proof that there are infinite primes resides in this cumulative process, as the addition of one to the product of any number of primes is either a new prime or it has a new prime factor. There are infinitely many primes. The infinite number of novel primes generates an infinite number of harmonies (i.e. multiples as in musical otaves).

Numbers are thus generated by two fundamental process of accumulation, the addition of one and the multiplication by primes. How these two processes relate is a central issue of number theory and more generally of natural processes. Multiplication relates directly to rotational processes. For instance, the numbers on a clock correspond to the multiples of twelve. Gauss [Gauss (1801)] introduced the generalization of clocks to number theory in the form of modular number systems.

Here we investigate the processes of accumulation and rotation in the generation of novelty by examining series generated by the accumulation of primes and approximations to the primes generated by progressive divisibility selections, and series generated by the Riemann’s equation. Riemann’s zeta function is a re-encoding of the structure of the prime numbers.

2 Methods

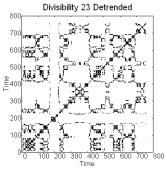
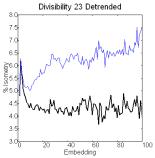
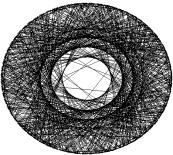
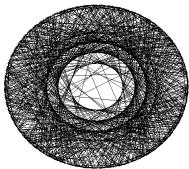
We study these series with the same methods for analysis used in a companion article [Sabelli, 2007] to study the primes. We look for complexes (clusters of isometries separated by interruptions of recurrence) in recurrence plots, novelty (less recurrence of isometric vectors in the series than in copies randomized by shuffling) in embedding plots, and the formation of concentric circles (“Mandala”) in complement plots. Trended series are detrended by subtracting the local average (ten consecutive members of the series centered in each point of the series).

3 Primes and Pseudoprimes

Let P(n) denote the nth prime number. As one detects and isolates the prime numbers from the series of integers by successively selecting and deleting the multiples of 2, 3, …P(n), we generate approximations to the primes by progressive divisibility selections, i.e. all integers except those divisible by the prime number P(n), which we shall denote as divisibility factor, and all primes less that P(n) (e.g. divisibility 7 means the series of integers from 2 to N [for some chosen N] when the multiples of 2, 3, 5, and 7 are filtered out).

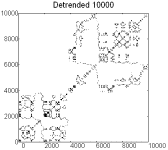
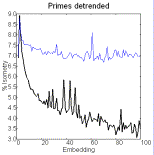
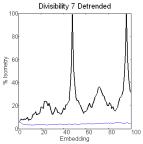
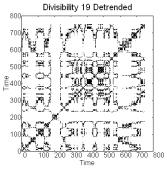
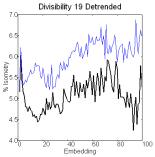
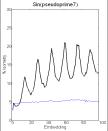
Detrended series of primes generate biotic patterns characterized by complexes in recurrence plots, novelty in embedding plots and a pattern of concentric circles in complement plots (Figure 1 top). Pseudoprimes generate periodic patterns characterized by complexes in recurrence plots and periodic peaks of recurrences in embedding plots for small P(n). 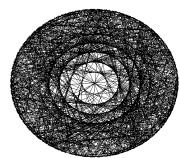For larger P(n), the series show biotic patterns, which consistently show less recurrence than their shuffled copies (novelty). As P(n) increases, complexes become smaller, novelty increases, and there is a larger number of concentric circles in complement plots. This is because larger differences between consecutive numbers generate smaller concentric circles. Such pattern of multiple circles indicates, in our view, the existence of a finite number of rotational generators. What is not obvious is why there is a finite number of circles even when plotting primes.

4 Cumulative series of primes and pseudoprimes

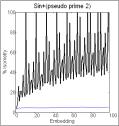
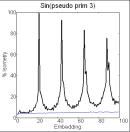
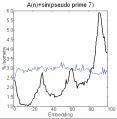
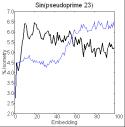
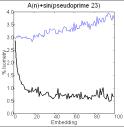
The series A(n) = sin(P(n)), where P(n) is the n^th prime, is chaotic. In contrast, biotic patterns are generated by A(n+1) = A(n) + sin(P(n)) (figure 2). Note the periodicity (indicated by peaks in the embedding plot) when the divisibility factor is small. When the divisibility factor is 7, some periodicity still remains but there also is novelty (number of isometries less than in shuffled version) and at still larger divisibility factors the periodicity disappears and the novelty becomes more pronounced.

Figure 1. Recurrence plots (50 embeddings, cutoff radius 1, 300,000 comparisons) [left], embedding plots [center] where the think line represents the series and the thin line the shuffled copy, and complement plots [right] of detrended series of primes and pseudoprimes.

Similar series constructed by accumulating prime differences after detrending also show structured recurrence plots and novelty (figure 3). The demonstration of pattern in the series of differences shows that the series itself is not stochastic, i.e. it is not generated by patterned changes not random ones.

Figure 2. Recurrence and embedding plots of the series of sin(prime or pseudoprime) [left two columns] and of their sum [right two columns].

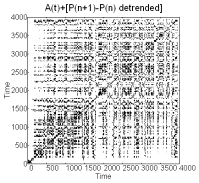
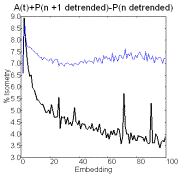
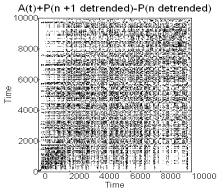
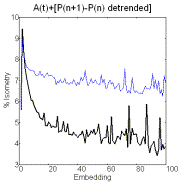
Figure 3 Recurrence and embedding plot for the accumulation of prime differences.

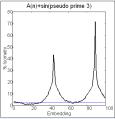
Again we see biotic patterns in approximations to the primes by sieving out only a finite number of prime multiples from the natural numbers and one can see these approximation approach the properties of the actual series for the primes as we increase the divisibility factor. Series generated by A(n+1) = A(n) + sin(P(n)), where P(n) are pseudoprimes, are periodic when the divisibility factor is small, and biotic for series generated with a large divisibility factor (figure 2). For relatively small divisibility factors, the series A(n+1) = sin(P(n)) and A(n+1) = A(n) + sin(P(n)), are initially more complex (figure 4).

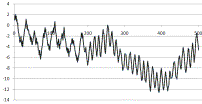
Figure 4. Time series of A(n+1) = sin(P(n)) [left] and A(n+1) = A(n) + sin(P(n)) [right].

5 Riemann’s zeta function

The Riemann zeta function is predated by the following series considered by Euler. The Euler series is the sum of the reciprocals of the positive integers:

S(N)=1+ 1/2 + 1/3 + 1/4 + …+ 1/N

where N is a positive integer. Euler considers the limit of this series as N goes to infinity. It turns out that the limit goes to infinity. The finite series S(N) diverges very slowly as N grows. Nevertheless it is of interest to write the divergent infinite series E=1+ 1/2 + 1/3 + 1/4 + …, for this formal series is intimately connected with the prime numbers. Note that for large N, sin(1/N) is approximately 1/N. Thus we can regard the Euler series as essentially the same as the result of accumulating sin(1/N) as N ranges over the positive integers. While the series of A(n+1) = sin(P(n) and A(n+1) = A(n) + sin(P(n) are very complex, the corresponding series for sin(1/P(n)) are not complex and just become progressively larger. On the other hand if we accumulate the sine of 1/N^s, then complexity will return in the form of the behavior of the zeta function that we will discuss below.

Euler showed the following formula

E = [1/(1-1/2)] * [1/(1-1/3)] * [1/(1-1/5)] * [1/(1-1/7)] * ... [1/(1-1/P(n)]…

where P(n) is a prime. Since E diverges, there must be an infinite number of primes for this formula to hold. In this way Euler proved in a new way that there are infinitely many primes.

Riemann and Euler generalized the series summing the reciprocals of the natural numbers to a function Zeta(s) by taking the sum of the reciprocals of the natural numbers raised to the power of s. That is,

Zeta(s) = 1 + 1/2^s + 1/3^s + 1/4^s + ...

The relationship with the prime numbers still holds, and one has

Zeta(s) = [1/(1-1/2^s)] * [1/(1-1/3^s)] * [1/(1-1/5^s)] * [1/(1-1/7^s)] * ... [1/(1-1/P(n)^s]…

For many values of s, the Zeta function converges to a specific value. Euler proved that

Zeta(2) = (Pi²)/6,

a remarkable result. Riemann extended the Zeta function to complex values of s. That is, following Riemann, we can take s = a + bi where i² = -1 and a and b are real numbers. Riemann then investigated the zeroes of Zeta(s) and found a series of zeroes on the negative real axis (these are usually called the “trivial” zeros of Zeta), and he made the conjecture that all the remaining zeroes are of the form

(1/2) + it

for certain real numbers t. This conjecture remains unproved to this day. It is called the Riemann Hypothesis. Here we examine series are generated by taking real and imaginary parts of the zeta function evaluated at the half line s= ½ + it.

We find biotic behavior in series generated from the Riemann’s zeta function. Both the real and the imaginary parts show structure in recurrence plots and novelty in embedding plots (figure 5).

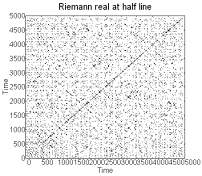
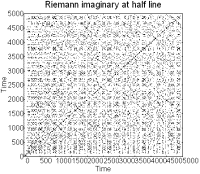
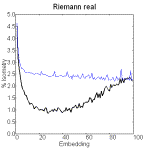
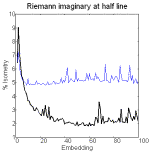
Figure 5. Recurrence and embedding plots of the Riemann zeta function at the half line.

One can also demonstrate evidence of periodicity in complement plots of the Riemann zeta function, but as the numbers are small are not integers, one must multiply them by a factor and round them (figure 6).

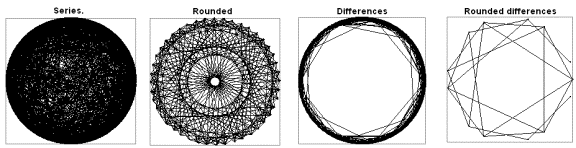
Figure 6. Complement plots of the real component of Riemann’s function and of the series of differences between consecutive terms and their rounded copies after expanding the series by multiplication by 20. N = 2000.

6 Discussion

These studies show how the biotic patterns observed in the primes are revealed by successive sieving of the integer series, and that they are also present in Riemann’s zeta function. Further they show evidence for the role of cumulative and rotational processes. These conclusions are consistent with ongoing studies on the prime number series and the Riemann zeta function. Both periodicity and fractality can be demonstrated in series related to the primes. Both appear in the statistics of the Goldbach partition [Wang et al., 2006]. Several studies have demonstrated the relevance of periodic functions. There are periodic oscillations in the histogram of differences of consecutive primes. The zeros of the Riemann zeta-function can be regarded as harmonic frequencies (via Fourier transform) in the distribution of primes.

Just as bios is fractal, so is the zeta function [Woon, 1994]. The spacings between successive zeroes seem to have a Hurst exponent of about 0.095, implying anti-persistence and high fractal dimension [Shanker, 2006]. While this is observed in fractional Brownian motion, these features are also present in bios. Obviously primes are generated causally rather than by the addition of random changes. The series of differences between consecutive terms of noise is random. The differences between consecutive terms of a biotic series are chaotic [Sabelli, 2005]. Chaos phenomena have been found in the difference of prime numbers [Ares and Castro, 2006]. These authors proposed a theory to account for the periodic behavior seen in the consecutive differences between prime numbers that links with the Hardy-Littlewood conjecture concerning the number of primes in intervals, the statistical mechanics of spin systems, and the Sierpinski fractal.

Schlesinger [1986] has recast Riemann's Hypothesis into a probabilistic framework connected to the fractal behavior of a lattice random walk. We propose instead to cast it as a biotic process generated by cumulative and rotational processes. The theoretical importance of this formulation lies to its connection to undulatory physical processes. The practical importance of this rotational process may be related to Shor’s quantum computational algorithm for factorization [Shor, 1997].

Assuming that numbers abstract basic properties of physical action, it is tempting to relate the cumulative and rotational aspects of these numerical processes to the corresponding properties of time described by [Gould (1987)]. The evolution of space-time appears to be chaotic [Cornish and Levin, 1997], not random. Aref'eva and Volovich [2007] have proposed a quantization of the Riemann zeta function and relate it to classical and quantum field theories as well as to string cosmological models. Connes [1998] suggests that the distribution of the Rieman zeroes is in the pattern of a radiative absorption spectrum. Berry and Keating [1999] suggest that the zeroes of the zeta function are in correspondence with the energy levels of a quantum mechanical system.

In summary, the study of primes and related series indicates that these mathematical processes are fundamental examples of causal creativity apparently generated by biotic processes of accumulation and rotation, and that these processes are intimately related to the properties of physical systems.

Acknowledgements: This research was supported by generous gifts from Ms. Maria McCormick to the Society for the Advancement of Clinical Philosophy.

Bibliography

[1] Ares, S. & Castro, M., 2006, “Hidden structure in the randomness of the prime number sequence?” , Physica A 360 285-296.

[2] Aref'eva,I. Ya. & Volovich, I. V., 2007, Quantization of the Rieman Zeta-Function and cosmology , arXiv:hep-th/0701284v2

[3] Berry, M. V. & Keating, J.P, 1999, H = xp and the Rieman zeroes, in SUSY and Trace Formulae – Chaos and Disorder, ed. Lerner et al, Kluwer.

[4] Connes, A. ,1998, Trace formula in noncommutative geometry and the zeroes of the Rieman zeta function, math.NT/981166

[5] Cornish N. & Levin J., 1996, The mixmaster universe: A chaotic Farey tale.

General Relativity and Quantum Cosmology, Phys.Rev. D55 (1997) 7489-7510, arXiv:gr-qc/9612066v1

[6] Gauss, C. F., 1801 and 1965, Disquistiones Arithmeticae, tr. Arthur A. Clarke, Yale Univ. Press.

[7] Gould, S. J., 1987, Time’s Arrow, Time’s Cycle. Harvard University Press.

[8] Kauffman, L. & Sabelli, H., 1998, The Process equation. Cybernetics and Systems 29 (4): 345-362.

[9] Kauffman, L. & H. Sabelli, 2003, Mathematical Bios. Kybernetes 31 1418-1428.

[10] Sabelli, H. , 2005, Bios. A Study of Creation World Scientific. Series on Knots and Everything, Vol 35.

[11] Sabelli, H., 2007, The Biotic Pattern of Prime Numbers Supports the Bios Theory of Creative Evolution from Radiation to Complexity. Proceedings of the International Conference on Complex Systems. Inter.Journal.

[12] Sabelli, H. & Kauffman, L., 1999, The Process Equation: Formulating And Testing The Process Theory Of Systems. Cybernetics and Systems 30: 261-294.

[13] Shanker, O., 2006, "Zeroes of Riemann zeta function and Hurst exponent" (preprint 01/06). http://www.geocities.com/oshanker/RiemannZeta/ZetaFunctions.htm.

[14] Schlesinger, M., 1986, "On the Riemann hypothesis: a fractal random walk approach", Physica A 138, 310-319.

[15] Shor, P. W., 1997, Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Computing 26: 1484-1509.

[16] Wang L. & Huang Y. & Dai Z., 2006, "Fractal in the statistics of Goldbach partition" (preprint).

OTHER CITATIONS THAT MAY BE NEEDED

S. Ares and M. Castro, "Hidden structure in the randomness of the prime number sequence?", Physica A 360 (2006) 285

C. Bonanno and M.S. Mega, "Toward a dynamical model for prime numbers" Chaos, Solitons and Fractals 20 (2004) 107-118

Jung, C. G. (1967, 1969). Collected Works, Vol. 5: Symbols of Transformation, 2nd edition, Princeton: Princeton University Press. Vol. 9: The Archetypes of the Collective Unconscious. Princeton: Princeton University Press.

Kauffman, L. H. and Sabelli, H. Riemann’s zeta function and the prime series display a biotic pattern of diversification, novelty, and complexity BABABABBABABAB

Levy, A.; Alden, D.; Levy, C. Biotic patterns in music. Society for Chaos Theory in Psychology and Life Sciences Meeting, 2006.

Patel, M. and H. Sabelli. Autocorrelation And Frequency Analysis Differentiate Cardiac And Economic Bios From 1/F Noise. Kybernetes. 32: 692-702, 2003

Sabelli, H. 2000. Complement plots: analyzing opposites reveals Mandala-like patterns in human heartbeats. International Journal of General Systems 29 (5): 799-830.

Sabelli, H. 2001 The Co-Creation Hypothesis. In Understanding Complexity. Ed. by G. Ragsdell and J. Wilby. Kluwer Academics/Plenum Publishers. London.

Sabelli, H. (2001). Novelty, a Measure of Creative Organization in Natural and Mathematical Time Series. Nonlinear Dynamics, Psychology, and Life Sciences. 5: 89-113.

Sabelli, H. Bios. A Study of Creation. World Scientific. 2005.

Sabelli H and L. Carlson-Sabelli. Bios, a Process Approach to Living System Theory. In honor to James and Jessie Miller. Systems Research and Behavioral Science 23: 323-336, 2005.

H. Sabelli, A. Sugerman, L. Kovacevic, L. Kauffman, L. Carlson-Sabelli, M. Patel, and J. Konecki. Bios Data Analyzer. Nonlinear Dynamics, Psychology and the Life Sciences 9: 505-538, 2005.

Sabelli, H and L. Kovacevic. Quantum Bios and Biotic Complexity in the Distribution of Galaxies. Complexity 11: 14-25, 2006.

Sabelli, H and L. Kovacevic. Biotic Population Dynamics and the Theory of Evolution. Proceedings of the International Conference on Complex Systems. NECSI. Inter.Journal 2006

http://www.interjournal.org/manuscript_abstract.php?82762892

Gerald H. Thomas, Hector Sabelli, Louis H. Kauffman, and Lazar Kovacevic. Biotic patterns in Schrödinger’s equation and the evolution of the universe. Inter.Journal 2006 http://www.interjournal.org/manuscript_abstract.php?1161328888

Sabelli, H and L. Kovacevic. Biotic population dynamics. (Accepted for publication, Complexity)

H. Sabelli and Gerald Thomas. The Future Quantum Computer: Biotic Complexity. In Reflecting Interfaces: The Complex Coevolution of Information Technology Ecosystems. Edited by F. Orsucci and N. Sala. Idea Group, Hershey. (in press)

H. Sabelli. Bios Theory of Physical, Biological and Human Evolution. In Explorations in Complexity Thinking. Edited by Kurt A. Richardson & Paul Cilliers. ISBN: 0979168813. ISCE Publishing (2007)

Sabelli, H and A. Abouzeid. Definition and Empirical Characterization of Creative Processes. Nonlinear dynamics, Psychology and the Life Sciences. 7(1): 35-47, 2003.

O Shanker 2006 Random matrices, generalized zeta functions and self-similarity of zero distributions. J. Phys. A: Math. Gen. 39 13983-13997

M. Shlesinger, On the Riemann hypothesis: a fractal random walk approach, Physica A 138 (1986) 310-319

Thomas, G.; Sabelli, H.; Kauffman, L.; Kovacevic, L. Biotic patterns in the Schrödinger’s equation and the early universe. Inter.Journal 2006 http://www.interjournal.org/manuscript_abstract.php?1161328888

M. Wolf, "Multifractality of prime numbers", Physica A 160 (1989) 24-42.

M. Wolf, "1/f noise in the distribution of prime numbers", Physica A 241 (1997), 493-499.

M. Wolf, "Random walk on the prime numbers", Physica A 250 (1998) 335.

S.C. Woon, "Period-harmonic-tupling jumps to chaos and fractal-scaling in a class of series", Chaos, Solitons and Fractals 5 (1) (1995) 125.