CHAOS, BIFURCATIONS, & SELF-ORGANIZATION:
DYNAMICAL EXTENSIONS OF NEUROLOGICAL POSITIVISM & ECOLOGICAL PSYCHOLOGY
FREDERICK DAVID ABRAHAM
Blueberry Brain Institute & Chaos Cooperative
http://www.pacweb.com/blueberry/
Based on invited lectures at the
Centennial Conference of the American Psychological Association, 1992, and the
Second Annual Conference of the Society for Chaos Theory in Psychology, 1992.
Reprinted from Psychoscience, 1(2), 85-118, ©Frederick David Abraham
ABSTRACT
Neurological positivism regards phenomenology, brain, behavior, and environment as a holistic unity. Their complex interaction over time can be regarded as a complex dynamical system, which we might call mind. Attractors and other features of dynamical systems can represent processes of the mind. `Insensitivity to initial conditions' suggests that the similar patterns made by different trajectories obeying the same invariant properties of a chaotic attractor and can be considered equivalent to represent such a given process of the mind. Degree of awareness is related to the magnitude of attractors. Jumps in magnitude (plosive bifurcations) result in saltatory jumps in awareness. The attractors of the mind may also undergo subtle bifurcations among various stable fixed, periodic, and chaotic possibilities. Ontogeny and phylogeny emphasize irreversibility of sequences of such bifurcations. Conscious control and effort can be invested in self-organizational control of such bifurcations which empowers the growth potential of individuals and societies. The power of the dynamical systems approach to provide both an easily communicable visual geometric language and a metamodeling strategy for the science and practice of psychology is providing support for the metaparidigm shift currently under way in psychology. The dynamical approach has implications for the evolution toward a better balance between unification and diversity in psychology, for gaining additional perspective on the free will issue, and for an increasing sensitivity to the humanist mission of psychology.
THE HOLISTIC MIND AS A COMPLEX DYNAMICAL SYSTEM
Vandervert (1993) has developed neurological positivism as a dynamical systems' world view. The fundamental assertions of neurological positivism seem so obvious and inevitable that their depth and revolutionary nature seem easy to undervalue. The most fundamental assertion is that there is a holistic unity involving mind, brain, behavior, and environment. None can be understood as a separate entity. Their mutually interactive and complex processes comprise an organic entity.
This view flows directly from a commitment to dynamical systems' theory. So does the view of ecological psychology proposed by Kugler et al. (1990) with their dynamical extension of Gibson's ecological physics (Gibson, 1979: Stoffregen, Schmuckler, & Gibson, 1987).
It might be noted that the term "Chaos theory" has come to represent the mathematical discipline of "dynamical systems' theory", of which it properly is a subset. This convention arises partly because of popular usage, partly because of the importance of chaos in so much of our universe, and partly because of the greater accessibility of contemporary dynamics, its greater communicability as a simple, coherent, unified geometric language (Leibniz, 1666; Leibniz & Abraham, 1995), than previous flavors of systems' theory. One might properly say that dynamical systems' theory (or more simply "dynamics") becomes a metamodeling strategy in science (Abraham, Abraham, & Shaw, 1990; Abraham & Gilgen, 1995), that is mainly a tool, albeit a very potent one, and that the neurological positivistic position yields itself to it. I am making a stronger statement, that the dynamical systems' point of view extrapolates to a world view. That view empowers a more realistic appraisal of complexity. As either or both, a strategy and a philosophical position, it is both necessary and sufficient for the establishment of a neurological positivism.
A brief review of a few basic ideas of chaos theory may show this obvious conceptual synergy. Dynamics takes a complex set of interrelated phenomena, observes the pattern of their behavior over time, and attempts to model them. As with any modeling enterprise, it measures arbitrary aspects (observable variables) of those phenomena (the system), and defines rules how the change of behavior of each variable occurs (usually with a set of differential or difference equations, one for each variable; but often a graphic sketch must make do) given each state of the system (a state of the system is one realization of the system, specified by the vector of values, one from each variable at that point in time). It may additionally invent, depending on your brand of positivism, hypothetical variables (Marx, 1951). The equations or rules of change involve the dependency of some or all of the variables on some or all of the others, and thereby represent the mutually interactive features of the system. They also involve nonlinear features that endow or summarize the ability of the system to show certain complex behaviors, such as transformations (bifurcations) and chaos.
The selection and definition of variables, both observed and hypothetical, is at once both very crucial and very arbitrary. Very crucial for clearly understanding components of the system, but yet arbitrary for a couple of reasons. One is the impossibility of specifying observables that best represent hypotheticals. Another is the difficulty of specifying the boundaries between the measured variable and the processes it is imbedded in. And the third is that even an inadequate set of observables may reveal many important properties about the behavior of a complex system. Variables thus often are chosen for explanatory convenience and their reification should often be engramed in salt.
Thus, for any given individual, the distinctions between environment, brain, mind, and behavior, while serving a convenient heuristic service, can be seen in some sense to be arbitrary. And none can be defined without reference to the other (as true for you and I as for Schrödinger's cat). Internal environment, response produced stimuli, proprioception, centrifugal control (in the nervous system), cognitive attribution, psychoneuroimmunology, are but a few of the concerns of psychology that show the difficulty of these distinctions. Even the simple term "response" stands for an interaction between organism and environment. The term "arbitrary" is not the same as "stupid"; it merely focuses on our discomfort in selecting one feature at the expense of selecting some other that might be more significant, or in forcing our conceptual isolation of that feature despite its strong embedding within a complex which might better be considered as a whole. It might be added that the dynamical sytem's point of view of the holism of phenomenology, brain, behavior, and environment, while fulfilling the requirements of positivism, are also consistent with philosophic positions that transcend positivistic limitations. They are holistic and complex within an analytic, positivistic approach, but are also compatible with more hermeneutic and phenomenological approaches was well. Disparate approaches can share a more unified understanding within psychology by using dynamics.
A dynamical system is defined as a vectorfield of the tendencies of the system to change at every state of the system. With the passage of time, the system passes through a succession of states after a given initial state is specified This path is called a trajectory in the state space. The collection of all such trajectories is called a portrait. Portraits reveal certain features. For example, all nearby trajectories may depart from a given point or cycle (called a point or periodic repellor). Similarly, all nearby trajectories may approach a point or a cycle (point or periodic attractor). Saddle points and cycles are points or cycles to which some trajectories approach and others depart. If there is more than one attractor in a portrait, basins are comprised of the trajectories going to each, and trajectories not tending to any attractor are separatrices (often forming the boundaries between basins). Chaotic attractors exist in regions in the state space and are neither fixed point nor periodic attractors, and they can vary between nearly periodic, to almost totally random. Their complex patterns come from the resolution of muliple tendencies or forces that both attract trajectories to a complex surface folded into a region of the space (convergence), and repel trajectories that cause neighboring trajectories to diverge from each other along the attractive surface (divergence). This divergence from even very close neighboring starting points is the famous `sensitivity to initial conditions'.
Attractors of the Mind
Even if it is impossible, as yet, to competently describe the mind, it is possible to discuss some of its properties from the conjectures evolving from dynamical systems' theory, even though there is only meager experimental support as yet. When William James borrowed Heraclitus' metaphor to describe thoughts as a `stream of consciousness', and further as possessing fast `transitive' parts and slow `substantive' parts (conclusions), he observed:
`Let anyone try to cut a thought across the middle and get a look at its section, and he will see how difficult the introspective observation of the transitive tracts is.' (James, 1890, pp 243-244.)
Actually, if the stream of thought can be represented by a chaotic attractor, there is a technique of looking at successive crossings of the trajectory through Poincaré's and Lorenz' sections (a plane in the state space). Poincaré, a contemporary of James, was the first to derive mathematical concepts of chaos while winning (or rather while correcting his winning) the prize from King Oscar's contest to show the stability of the solar system and thus reveal God's orderly hand. With Poincaré's and Lorenz' sections, as with James' section, one cannot infer much from a single crossing of the trajectory, but, from a multitude of crossings, one can infer a great deal about the nature and complexity of the attractor, including its fractal nature. That is, the pattern of successive crossings of a chaotic trajectory across a Lorenz plane often reveals a fractal character, which represents the communality between dynamics and fractals.
Time and Insensitivity to Initial Conditions
By implying that many aspects of mind are attractrors arising from interactions of phenomenolgical, behavioral, neural, and environmental processes as a nonlinear dynamical system, there are a number of other benefits and problems that accrue from this metaphor. If a memory is a chaotic attractor, by definition it requires time for expression. How much time does it take the brain to process an attractor? Over how much time must it integrate to comprehend the attractor? If the mind cannot comprehend an instant in time, what kind of time spans are required and is it capable of? There has been much discussion of this perplexing issue, and it is raised in part to emphasize the more resolvable context of the dynamical systems' point of view, but even more to relate it to the context of the discriminability between attractors representing different processes of mind such as specific memories. It is tempting to say `state of mind' instead of `process of mind', but "state" is a technical term of dynamics that represents a system at a given instant of time.
The `sensitivity to initial conditions' previously mentioned, could lead one astray into believing a strict requirement that only one specific trajectory (or all of them) from a chaotic attractor could represent a process of MIND such as a memory. Remember that many trajectories from very diverse locations approach the attractive surface of a chaotic attractor, and while neighboring trajectories diverge along the attractive surface as they progress in time, they all obey the same laws (vectorfields), and make very similar patterns, despite being at different places within the attractor at any given time. It is also true that all trajectories eventually pierce an arbitrarily small volume of the attractor so the ability to gain information about past states of the system from knowing the small volume within which a trajectory passes is limited to fairly local time.
My contention is that the attractive properties, the complex pattern in general, the attractor, represents a process of mind. That is, not a specific trajectory, but any trajectory from that attractor, may adequately represent it. The exact starting time and location in a train of thought or stream of consciousness, and its exact spatio-temporal location as say in a given neural circuit reusing the same set of neurons, is unimportant. I call this `insensitivity to initial conditions'. It is to be admitted that no one has specified exactly an attractor for a given memory, or any process of mind, or how different attractors need to be for discriminability between different processes. Within the brain, this insensitivity is an extension of Lashley's concept of `equipotentiality'. Skip Skinner has also conjectured that within the brain there may be generalized chaotic processes in memory storage:
"If data compression is the raison d'être for a chaotic dynamical process, and if information storage is by a `compressed representation' and not a specific `engram', will we finally be able to recognize biologically stored information?" (J.E. Skinner et al., 1990).
And Freeman, from his research on the olfactory bulb in odor discrimination, conjectures that an activated memory is a periodic attractor, and that the stored attractor is chaotic:
"I conceive the bulb as carrying a repertoire of learned limit cycle attractors.. Each is distinguished by its input basin with respect to receptors and by the spatial amplitude modulation pattern of its output. Random access is facilitated by the chaotic basal state, which keeps the bulb far from equilibrium and ready to move rapidly to any region of optimal convergence." (Freeman, 1990).
Mpitsos, from his work on the carnivorous marine mollusk, Pleurobranchia californica, also made a neurological positivistic extension of the equipotentiality concept, using chaotic attractors as the basis for multifunctionality of neuronal circuitry and behavioral blending which demonstrates that even that organism is integrating a view of the entire attractor:
". . . A set of neural connections may be able to generate many and variable attractors. Some of these may be adaptive for certain environmental demands, while others may have little adaptability. What determines the appropriate responses at any given time, we believe, is not the selection of a particular centrally programmed neural structure or attractor, but rather the process arising from the continual interaction between the animal and the environment. . . . When viewed in this way, the concept of attractor is scale-independent: it takes into account a variety of different types of activity that occur within single neurons, among groups of neurons, between areas of the brain, and through the interactions between the animal and the environment." (Mpitsos, 1990).
Lorenz (1963), who rediscovered `sensitivity to initial conditions', despaired that his now famous Lorenz attractor told him that exact weather prediction was impossible after a few days. Although he despaired, the mind of the tree didn't give much of a hoot how much rain or sunshine occurred on a given day; it cared only with weather patterns over weeks, seasons, and years had certain invariant properties. Don't despair, Lorenz, your attractor is telling us much about how mind works.
Parenthetically, this dynamical systems' point of view of James' `vigor', `stability', and `glare' may reflect the distinction between concepts of time that are nonlinear irreversible Bergsonian (Greek's chairos, Bergson's durée, Loye's timeless and spatial times) and linear Newtonian reversible (Greek's chronos, Loye's serial time). The temporally linear motion along a trajectory is obeying chronos, but the mind, integrating over periods of time, creates the saltatory evolutionary durée time of chairos (Loye, 1983; Wiener, 1948). This temporal factor is reflected in the distinction made in ecological physics between holonomic and nonholonomic constraints on intentional behavior (Kugler et al., 1990.):
"Holonomic constraints . . . can be expressed functionally as a relationship among coordinates, and thus do not materially alter the system. [Obeying rules of linear time.]
". . . if intentions are nonholonomic, then something like cognitively internalized models of the environment and the actor's place in it would have to be assumed . . ." [Obeying rules of nonlinear time.]
Summary One
To summarize thus far, we have seen that (1) mind can be considered an interaction of mentation, brain, behavior, and environment into a holistic unity, (2) mind can thus be represented by a dynamical system exhibiting any number of attractors and other features, (3) these attractors may represent a variety of `processes of mind', (4) the processes of mind are functionally effective not for a given moment; but rather they require some integration over time, and (5) `insensitivity to initial conditions' summarizes that several different trajectories performing in the same attractor may equivalently represent a given process, to a certain extent, independent of particular time and place.
BIFURCATIONS AND THE ONTOGENY OF MIND
At this point it is useful to introduce another basic concept of dynamics, that of bifurcations. Dynamical systems can change. As the vectorfield changes, so does the picture of the results of integrating it over time, the portrait. The changes implied under the term bifurcation are when some parameter of the system are changed (rather than the variables and equations themselves). That is, the equations retain their same form, but the value of some constant changes. A parameter can be changed over a large range of values while the portrait changes but gradually. But then, the value of the control parameter may change by a very small amount resulting in a radical transformation in the systems' behavior. Such a transformation is called a `bifurcation'. There are three main species of bifurcations. A subtle bifurcation is where one type of attractor changes to another, as when a fixed point attractor changes to a periodic attractor in a Hopf bifurcation. A catastrophic bifurcation occurs when an attractor either appears or disappears. A plosive bifurcation is when there is the sudden shift in the magnitude of the attractor. As with chaos, bifurcations can only occur in nonlinear dynamical systems (where at least one of the differential equations is nonlinear).
Cognitive Bifurcations and Awareness
If you review the quotes of Skip Skinner and Walter Freeman above, you will see that they mention bifurcations in memory packaging, storage, and retrieval. Skinner alludes to a chaotic recursive algorithmic packaging and unpackaging of complex information in memory storage and retrieval similar to the affine mapping procedure developed by Barnsley (1988). Such a procedure would certainly imply subtle or catastrophic bifurcations with plosive features. From Freeman's quote, it is not entirely clear whether the periodic attractor bifurcates subltly to a chaotic attractor or undergoes an implosive miniaturization becoming imbedded in and temporarily trivialized but nurtured by surrounding chaotic activity.
This procedure could be generalized. If a process of mind is a chaotic attractor, then when it slips away from awareness to be packed away until recollected, that may well be an implosive bifurcation: it remains pretty much the same but is a greatly diminished, yet ongoing, dynamic process. Or there may be a subtle bifurcation with implosive features. The reactivation of such a memorialized attractor is the explosive counterpart. In terms of our awareness, these implosive and explosive events seem like catastrophic bifurcations, appearing and disappearing in and out of the blue, as when the whereabouts of a misplaced object suddenly reveals itself, and once put back in our pocket, is forgotten. Of course, as much of depth and dynamical psychology has stressed, there may be quite a life to the continued dynamics of the processes of these attractors while they are hidden from awareness.
I wish mainly to emphasize that from this point of view, awareness and consciousness could be thought of as on a continuum that depends, among other things, upon how much of the relevant portions of the brain are brought into play, which also, from the dynamical concept of mind, means how much of the mental, neural, behavioral, and environmental acivity are being brought into play. Despite the degree of awareness being a continuum, the suddenness of shifts in it arises from the suddenness of bifurcations in nonlinear dynamical systems. There are, obviously, also gradual changes in degree of awareness and the amount of energy expended on a particular process. In general the expansion of an attractor requires that more energy be devoted to it; increased forces increase the magnitude of the vectors of the vectorfield. And conversely, the shrinkage of attractor is accompanied by the lessening of energy requirements by the system.
These features recall another property of dynamical systems, namely those relating to stability. Originally, homeostasis, a fixed point attractor, was considered the only type of stable attractor in biological and behavioral science. More recently, stability has been considered liberalized to include psychobiological periodic and chaotic attractors. It is now recognized that chaotic attractors may represent normal, desirable, processes. Instability occurs at bifurcation points, when an existing attractor breaks up and dissappears. The system is very unstable with a characteristic portrait at that bifurcation point, and any small change in the control parameter and thus the vectorfield, pushes the system quickly to either side of the bifurcation point, where its character may be revealed by a new portrait. A dynamical scheme is a dynamical system as a function of one or more control parameters and can be visualized as a response diagram, which usually features a bifurcation sequence (Fig. 1). Bifurcation diagrams are similar but graphically ghost out all trajectories except those representing the attractors themselves, in order to emphasize the bifurcation sequence.
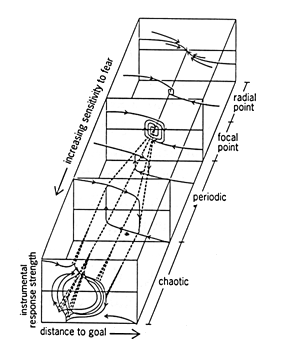
|
| Figure 1. Response diagram for a dynamical scheme for a nonlinear model of internal approach-avoidance conflict. The vertical planes each show a state space with some trajectories from a portrait for a dynamical system. The axes of these state spaces are the strength of behavior (observable or cognitive, on the vertical axis), and the nearness to a goal that is both feared and desired (conflict; on the horizontal axis). The axis perpendicular to the plane of the state space is the conrol parameter, here presumed as some general sensitivity to fear. Shown is a sequence of subtle bifurcations, first a Hopf (going from a fixed point to a periodic attractor), and then excitation of chaos (going from periodic to chaotic; the chaotic attractor is shown as the shadow of a trajectory that winds about a 3D torus. |
Implications from Developmental Psychology
Cairns (1990), in reviewing the outstanding book on child development by Cole and Cole 1989), summarized the `quiet revolution' occurring in this field as including:
(a) lifelong extension in which "Longitudinal procedures constitute the design of choice if one hopes to unravel the secrets of behavioral and cognitive mediation over time."
(b) systemization of its cross-cultural and comparative aspects,
(c) a need that "measurement and analytic strategies should be sensitive to developmental changes and the emergence of novel functions", and
(d) its essential nature as "The study of development requires a holistic, synthetic science. Maturational, experiential, [biological] and cultural contributions are inseparably coalesced in ontogeny. Hence developmental studies should be multi-level, concerned with ontogenetic integration, and employ person-oriented as well as variable-oriented analyses."
The similarity of these ideas to those of the dynamical systems' point of view are all too obvious. Point (a) simply reflects that bifurcation sequences continue through life; trajectories need be studied lifelong. Point (b) stresses the holistic interaction of world and mind and the coupling of individuals to cultural systems. Point (c) says look for the bifurcations, especially creative catastrophic ones, and literally begs for the dynamical strategy. And finally, point (d) is a straight forward description of the program of the dynamical point of view. A considerable amount of developmental research has incorporated the dynamical systems' point of view as central to their programs.
In cosmological, biological, and mental development, while some bifurcations may be in some sense reversible, especially if one permits some generalization of attractor types as functionally equivalent and therefore an acceptable exception to the Herclitan/Jamesian stream metaphor, there seems to be an irreversible bifurcation sequence toward increased complexity. As Smith (1995) says in discussing the dynamics of children interpreting novel words (never previously encountered) from context:
"Thus children's novel word interpretation exhibit both a global sturcture and local adaptability because these interpretations emerge in context as the result of a nonlinear attentional system that creates new solutions from past experiences and the particular properties of the perceptually present. Stability and variability emerge as joint products of real time process." (Smith, 1995)
Fogel (1988) also observes a critical ontological bifurcation:
". . . a stable emergent state of gazing away from mother can be created in pre-sitting infants who can reach simply by experimentally providing the missing control parameter of sitting upright. This stable state cannot be created by the postural manipulation in pre-reaching infants. The supine behavior of pre-sitting infants who can reach for objects shows both within and between individual variability characteristic of critical fluctuations of a dynamic system in a transition region between two stable states.
And Thelen (1988) further discusses the nature of ontological time, and the requirements of dynamical research upon it:
"If the dynamical principles of complex systems in real time can be extended to systems in developmental time, there are implications for both the conceptualization of development and for empirical studies. On the theoretical level, this means that development must be viewed as a series of more-or-less stable attractors that are task assembled, and where complexity arises as successive bifurcations that may be deterministic, but are not predetermined.
"Our empirical task is even more duanting. The first step toward a dynamical model of any developmental phenomenon is understanding the behavior of the collective variables over time. Here we face the nontrivial task of choosing the appropriate collective variable: how best to capture the compression of the degrees of freedom. As we extend the time scale, it is not clear that the psychological meaning of a collective variable remains stationary. The same behavior may mean different things at different ages. Thus, the trajectory of the collective variable must be plotted on an appropriate time scale.
"Because it is at the transition between new forms that we can explore the dynamics of developmental change, a dynamical understanding almost always requires intensive longitudinal studies.."
Viewing the ontogeny of both the mind as a shorter term aspect of mental life and as major long-term developments during life, reflects an increasing and irreversible complexification. In some sense, however, as mentioned, some bifurcations can be considered reversible, or better, repeatable given some liberty of generalization. A friend, a therapist, a parent, a teacher, a self, may recognize different recurring stable patterns of behavior in a person, may learn some relevant control parameters as well, and may learn to operate on these control parameters in such a manner as to create bifurcations away from less desired attractors or portraits, toward more desirable ones. The style, ethics, and morality of such control is of considerable interest, but shall be deferred for now. The extrapolation of James and Heraclitus would lead us to conclude that the attractor is never exactly the same stream. Weiner (1948) and Prigogine and Stengers (1984) have also emphasized the irreversibility of time the evolution of complex systems. An example of a control parameter for the evolutionary bifurcations to more complex phylogenetic minds could depend on something as simple as the increase in the amount certain iterative features brain, such as cortical, hippocampal, cerebellar, etc. mass.
For anohter example, Paar (1992), has suggested that creating confusion can be a useful therapeutic tool. Consider that an individual is stuck in an unpleasant personality condition or behavioral-cognitive attractor that nonetheless is stable and holds some security and from which the individual cannot find escape. Creating confusion then means creating a new problem (portrait) for the individual which is not familiar and whose relationship to the undesirable attractor is not clear. In so doing, the therapist has moved that individual closer to a bifurcation point, from which the individual may either fall back to old patterns (the therapy fails), or moves on to new ones (the therapy succeeds with a bifurcation to a new attractor). These changes are facilitated because the system at the bifurcation point is very unstable. Confusion, of course, is not the only strategy to get to the bifurcation point. And confusion is not the only condition that could be experienced at the bifurcation point. Hope for the help afforded by the expected change, or discomfort caused from experiencing the instability are but a couple of the additional possibilities. The instability is felt, new vectors are sought, one vacates the bifurcation point, hopefully, evolving to a more mature and fulfilling life style. The basic idea here is that the evolution of complexity may (a) move on to new attractors, new portraits, which may be quite novel, and (b) require the expenditure of some conscious effort in order to cross bifurcation points.
Note that confusion is not the same as chaos, which is perfectly at home in both stable, healthy, and desirable systems and in unstable, unhealthy, or undesirable ones. This is encapsulated in Abraham's First Protoplatitude:
For biopsychological systems, it is likely that all varieties of attractors can represent both desirable and undesirable and both normal and abnormal conditions. That is, knowing a psychological process is chaotic tells you nothing about whether it is healthy or not. (Abraham, Abraham, & Shaw, 1990, p. III-112)
To develop this theme further requires an additional aspect of dynamical systems' theory, but first a further comment on time is also needed.
Time Revisited: Linear Chronos in Bifurcational Instability;
Nonlinear-Chairos in Attractor Stability
The considerations of Smith, Thelen, and Paar concerning the instability of the bifurcation point, leads to a further observation on the distinction of the operation of processes of mind with respect to linear and nonlinear time. The instability of the bifurcation point leads the mind to have to deal with a briefly visited portrait, to struggle with it from the viewpoint of residing at a given point on a trajectory, navigating the trajectory from within the confusing and/or uncomfortable portrait (dynamical system, the vectorfield), which demands a great amount of energy be devoted to the linear time requirements of that task. The tennis player must watch an unusually approaching ball more carefully; the musician must read a new piece of music more carefully. The baby speaks its first word, takes its first step, a person is on the verge of entering or departing a close relationship or confronting a phobia.
At the bifurcation point, the trajectory requirements of chronos are very great. The chairos demands are also great as the response diagram is surveyed, and novel future projections are constructed, evaluated, and selected. After the bifurcation is successfully traversed and the trajectory now performs within a stable vectorfield, the chairos map of the attractor may dominate as the demands made by being on a trajectory become more familiar. There is a waxing and waning between the relative importance of linear and nonlinear time. This topic now also needs be put aside, to await the introduction of the concept of self-organization.
COMPLEX DYNAMICAL SYSTEMS, SELF, AND SELF-ORGANIZATION
Obviously, there may be several attractors of mind simultaneously active. An extreme example would be when a "fully commissurotomized person possesses two streams of consciousness" (Natsoulas, 1991). Or they may exist at differing levels of awareness, as with subliminal psychodynamic activation (Masling et al, 1991). There are a couple of important implications from these considerations. One is that these processes are active even when `miniaturized' might be accomplishing some important tasks. The second is that different processes may be communicating with each other (as in the subliminal psychodynamic activation on cognition, Masling et al., 1991).
Networks Coupled via Control Parameters
So now let's return briefly to the mode of reviewing basic concepts in order to see how dynamical systems' theory conceptualizes coupling within complex dynamical systems. Two or more dynamical schemes are considered coupled when the control parameters of one scheme are a function of the state of another system.
For example, a change in the anxiety-provoking value of a subliminal message results from a dynamical affective system, and the anxiety level from that affective system is a control parameter which causes a bifurcation in the cognitive recall/recognition system (Masling, 1991). This example follows the typical ploy of separating affective and cognitive subsystems.
The arbitrariness of the conceptualization of a network is greater than that mentioned earlier in the choice of variables, but in a sense, is more trivial in that the different conceptual networks possible from breaking down a larger set of interacting variables, or even lumping them all into a single system, are reasonably equivalent in terms of the behavior of the system, and represent mainly different ways of obtaining visual intuition for the modeler. But there is a convenience in recognizing that some parameter-variables are of significance as control parameters to some system or subsystem, that is, are responsible for bifurcations. The applications to concepts of consciousness are numerous (R. Abraham, 1990; Bütz, 1992, Combs, 1995; Conforti, 1994; Goerner, 1993; Macy, 1991; Mandell, 1980; Paar, 1992; Rossi, 1989; Sabelli, 1990). The interaction of the domains of consciousness present too vast an arena to explore adequately here. But there is an additional feature of complex dynamical systems that bring us to the most transcendental, agential, teleological, and humanistic features of mind and behavior. That feature is self-organization or self-control.
Self-Organization
The statement of the principle is deceptively brief, but most profound in its implications. It is an extension of the principle we just saw, that of the control parameter of one scheme being under the control of another. It is simply this: When the control parameters of a system are influenced by the state of the system itself, that is self-control, or self-organization
.
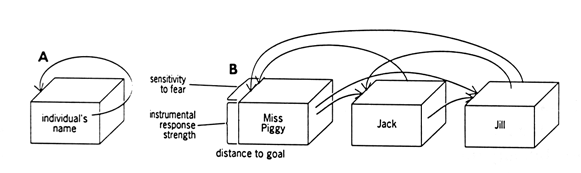
|
| Figure 2. Newtork Diagrams for
(A) Direct Self-Control and
(B) A Social System of Three Coupled Individuals.
Each individual has a version of the dynamical conflict system of Fig. 1 represented by each box and in which they share some common goals, e.g., going up the hill to fetch a pail of water; Jack and Jill had some trauma there also. Miss Piggy had none and is fearless. The arrowed lines show the influence the behavior that each has upon the control parameter of the others. In every instance, each is influenced by herself or himself indirectly. |
This self-control can be by means of an immediate route (Fig 2A), or by the mediation of a network of dynamical schemes (Fig 2B). Such a network is called a complex dynamical system. This concept transcends the usual concept of feedback. The ordinary garden variety concept of feedback, such as in the continual interplay of centrifugal brain control of sensory processing, and other features of the continual interplay of environment, brain, and behavior familiar to all students of the brain, are already incorporated into the notion of the interacting variables of a dynamical system. Rather, self-control focuses on the reorganizational features of systems, individuals, and societies. This reorganiation comes from the ability of a system to create its own bifurcations.
An example could be derived from the previous discussion in which it was suggested that levels of awareness were related not merely to the typical view of the involvement of thalamo-fronto-cortical activity, but the total amount of such activity. From this point of view, the result of Orme-Johnson (1977), that the increased coherence and EEG homogeneity of great areas of the cortex bilaterally during meditation, could indicate an attractor that was engaging a larger and greater focus of the mind/brain under self-regulation of a self that is seeking such expansion. Similarly, increased coherence in hypothalamic feeding systems (Abraham, 1997; Abraham et al, 1973); in behavioral-cortical sytems (Anderson & Mandell, 1996; Bressler, Coppola, & Nakamura, 1993), and in the development of cortical networks in gender development (Hanlon, 1996) are additional evidence of self-organizational dynamics.
Pribram, in his holonomic integrative view of how processes of the brain participate in perception, suggests that linear Gabor dynamic systems of perception combine with those of the self-organizational features of nonlinear dynamical systems to provide stable dynamic attractors in the brain.
"Brain processes are to a considerable extent optimally self-maintaining and even self-organizing (a point also made by Maturana, 1969 and by Varela, 1979) — and not subject only to the vagaries of input organization nor to spontaneous, unpredictable organization. . . Kohonen noted [Kohonen & Oja, 1987], where synaptic couplings are formed adaptively,.. the output state can relax to the linear range or to saturation [comment: fixed point attractor of the ordinary learning curve]. In Kohonen's model (1972, 1977) learning takes place in the linearized mode. (Pribram, 1991, pp 42-43.
In discussing the role of the amygdala in familiarization, habituation, orientation, arousal, learning, and the disruption of hierarchy in social systems of monkeys, he continues this analysis.
"Originally, we thought these stabilities described states of equilibrium . . . [but] stabilities far from equilibrium offered a much richer model: Perturbations of equilibrium states could only lead to a return to equilibrium; perturbations of states far from equilibrium would lead to the potential for achieving novel states of temporal stability.
"Stabilities far from equilibrium are attractive; they operate as attractors toward which the process tends.. [as] during learning — in experimental psychology terms, it values the act by means of a reinforcing process. In the holonomic brain theory, this process is mediated by the protocritic (pain and temperature) system." (Pribram, 1991, pp 218-219.)
The major historical learning theories involved linear equations, differential equations for drive-reduction theory (Hull, 1943); difference equations for statistical learning theory (Estes, 1959; Voeks, 1954).
The implications for psychology become exciting when extended to the notion of a person influencing her or his own behavior. If self-control is mediated by a social system, a network of communicating individuals, it might be easy for an individual to be unaware of such self-control. When a person directly adjusts her or his own control parameters, while this may involve unconscious processes, it more often involves conscious control. In either case, a learning of the system's behaviors at different values of the control parameter may occur. This learning implies the ability to discriminate along the control parameters, and to change them when necessary. Such learning can take place in social systems, and reveal how social systems can become personalized through the intervention of control parameters. Perhaps this can best be illustrated by a story of the Philippine Monobo (collected and performed by Priscilla Magdamo).
Palaas, the monitor lizard, leaves her friend, Salarung, the deer, baby-sitting while she forages in the river for food for her child. While Palaas is gone, something frightens Salarung and she prances about stepping on Palaas's baby, killing it. Upon her return, Palaas demands financial compensation from Salarung as the agent responsible for the death of her child. Salarung pleads that she was not agentially responsible for the death. They go to the the Timuay, the village chief, to adjudicate the dispute. There is a recursive passing of the blame among a sequence of agents who each testify before the Timuay. Ting Ting, the fireflies, scared Salarung to whom they seemed like fire in the forest. Ting Ting were aroused by Balansahan, the woodpecker, whose victory drumming was in response to Kulihi, the kite whose victory flight and cries were in response to Buaya, the crocodile who was sunning itself on a rock which Kulihi took to be a drying of the armor after a battle. However, Buaya, it turns out, was trying to escape the tickling of its undersides by, Urarang, the shrimp he thought were playing there. In reality, Urarang, considered Buaya a friend who would protect them from predation by their enemy who was out foraging for food for her child. That enemy? You guessed it: Palaas.
This story is told when a Timuay adjudicates disputes in which the blame can be derived back to the accuser. It is also part of the folklore, told by friends and parents to children. Thereby, this attractor is learned by the culture, and individuals learn to actively search for blame when a wrong is committed. Awareness or sensitivity to blame is itself a control parameter; the search for causal chains may be represented by other control parameters, and the strength of blame within self and among others are the variables in whose state space the attractor emerges. Some of the control parameters may be manipulated by others, as by the Timuay in a Monobo village, or as a reminder to a student by a principal in a Vermont school where the story has also been told. Or these control parameters are under adjustment by anyone confronting his or her own behavior before assigning guilt.
Schwalbe (1991) describes the autogenesis of the self as a bifurcation sequence of increasing order and complexity in which self-organization plays a key role. He suggests self-organization is the creation of new information in a dynamical system with the developement of increasing complexity. He confesses that while he cannot make the process entirely clear, "but placing the emphasis on the role of control parameters as the locus of self-control over bifurcational sequencing in self-organization should help make the modeling of the processes clearer." Schwalbe outlines a development of the self over four stages during the first two years of life: "the self-organization of neural networks; the selective capture of information by the body; the organization of impulses by imagery: and the organization of imagery by language."
The first depends on the brain.
". . . a coherent self . . . has to do with the brain's operation as a dynamical system in its own right. . . . there is mutual determination here: the organic structure of the [connection] matrix [of the brain] facilitates particular patterns of energy flow, which in turn affect the subsequent development of the matrix. . . [which] are are essential to the emergence of consciousness and a self."
With respect to the second stage involving the body as a selective system, he means that the system evaluates self-created information, its survival value, its potential, within envirnomental constraints.
"The outcome of autogenesis is determined, in other words, by the interaction between a body with certain selective capacities and an environment with certain information potentialities. Thus while self-organization in the brain is a partly autonomous process, autogenesis unfolds as it does only because the brain has a body to mediate between it and the external world."
In the third phase, dealing with the use of imagery, he describes a process that is analogous to that which I have characterized as the evolution of the mind's view of its own response diagram, not only the system, but its past, and its potential futures as well. When the brain develops the capacity for imagery, this imagery empowers a memory of body-environmental interactions.
"This allows . . . an awareness of awareness . . . the self and mind are going through a further stage of self-organization. . . the emergence of an autonomous consciousness capable of sustaining its own development." This imagery can modify itself or produce novel imagery which "thus engenders further self-organization. . . . once . . . the brain is developed to the point where imagery can be formed, then self-organization reaches a new level of efficacy. . . . Now a self that can continue to organize itself has emerged."
In the fourth phase of autogenesis, language comes to control imagery and self-representation, while passing from Vygotsky's 'outer speech' to 'inner speech', and language controls awareness via its control of the flow of imagery ". . . sustaining the integrity of the self as a complex dynamical system."
In terms of my formulation of mind, choice involves either exerting self-organization through control parameters under a higher-order chairos-durée temporal representation of the self as a complex dynamical system inhabited by a variety of attractors undergoing explosive and implosive bifurcations, or by repositioning oneself in the state space, selecting a new initial position to jump on a new trajectory. Usually choice is a combination of both. Schwalbe's post-autogenetic, autopoetic phase of development recognizes these modes, in the continued functioning of imagery and language in the changing of self.
"Because self-imagery is part of a nonlinear dynamical system, even slight changes in this imagery can have powerful reorganizing effects on all other `parts' of the self. . . The real value of the self lies, however, in the stability and adaptability it gives us. . . [It is] a creative force; because of its nature as a nonlinear dynamical system, it can use information it captures to drive its own evolution in unpredictable directions. It is the source of the surprises we continually provide ourselves."
Ecological physics also stresses the role of bifurcations among attractor patterns in a chairos-cognitive mode under self-organization:
". . . an intentional organism is constituted by a similar type of internally self-organizing mechanism. That is, there is an internal field within the organism that is organized by the layout of attractors. These attractors are goal states that act to constrain the system's internal degrees of freedom. The corresponding field, which is determined by the organism's effectivities (i.e., capabilities for action), embodies the internal constraints on action. A change in the number and layout of goal states will result in a change in the field, which in turn manifests itself as a qualitative shift in behavior mode
"The problem of intentional behavior cannot, however, be relegated solely to an internal-state description. For we saw previously that the phenomenon of intentional dynamics is only apparent at a more global scale — the ecological scale — because goal paths are ecological-field processes whose support depends upon the coupling of two fields — the external field of the environemnt and the internal field of the organism." (Kugler et al., 1990.)
Navigating the response diagram: therapy, mind, and time issues reviewed.
Now you can see why we interrupted a couple of topics. The discussion of Paar's confusion therapy was interrupted just at the point of making the obvious extension of turning over control to the patient. The concepts of networking and self-control also liberalize from the formal therapeutic situation to that of self-help and consciousness-raising groups, to the use of self-administered forms of realizing one's growth potential. From the neurological-ecological positivist's view of mind, including the study of brain, those forms of self-control that utilize meditation, biofeedback, altered states of consciousness, the search for peak experiences, etc. are in the forefront of using complex dynamical theory, but other cognitive approaches as well as behavioral-operational ones (Killeen, 1992) also utilize dyanmics. Paar and other therapists who have used the dynamical systems' point of view in therapy (Burlingame, 1995; Conforti, 1994; Elkaïm et al., 1987; Gampel, 1991; Langs & Badalamenti, 1991; Leven, 1992; Levine, Leven, & Prueitt, 1992; Mosca, 1995; Paar, 1992; Raphaely, 1990, Redington & Reidbord, 1993); Rindfuss et al., 1987); Sabelli, 1990; Swinney, 1991) have stressed the growth potential of the self-control of bifurcations to novel attractors.
It should also be evident why the discussion of consciousness was interrupted, for even more important than self-regulation of behavior within familiar territory of the self, is the extrapolation to to the inventing of such territory by using imagination and by making choices that empower our future to develop new selfs, to inhabit new attractors. One can boldly go where one has not previously ventured, exploring conjectured attractors, making informed choices concerning potential trajectories, and willing to make the bifurcational leaps, to grab the control sticks on those parameters, to see where the trajectory leads. This consititues Tillich's "courage to be" (1956), to affirm and create self (Abraham, 1996a). Loye has made especially noteworthy contributions to the study of mind in the use of the dynamical systems' point of view in projecting the future and making future-oriented choices (Loye, 1983).
The waxing and waning of the balance between linear and nonlinear time can now be seen under zoom self-control, not only in response to the changing demands of each as one approaches and departs bifurcation points, but by concentrating on time dilation and contraction itself as a control parameter. The tennis player, the musician, an individual entering meditation, is controlling time perception quite directly, and this is involved in a self-organizational process. Note the implication for the ability to perceive several time parameters simultaneously, and to self-organize by controlling one's position on this multidimensional control space.
Summary Two
(1) Awareness of processes of mind is related to the magnitude of attractors, which can change gradually or bifurcate. (2) Normal stable processes of the mind are often orderly chaotic processes. (3) Instability occurs at bifurcation points in complex dynamical systems including those participating in mind. (4) Considerations of ontogeny and phylogeny emphasize the irreversibility of many bifurcations sequences toward increased complexity of mind. (5) Therapeutic and transpersonal views emphasize the conscious control and effort needed for some growth bifurcations. (6) Bifucations under self-organization empower the growth potential of individuals (and societies). (7) The mind integrates over time a vision of potential response (and network) diagrams, and self-organization implies navigation of the control space for such diagrams, which includes maneuvering in a multidimensional control space of perceived linear and nonlinear time.
IMPLICATIONS FOR THE SOCIOLOGY AND PHILOSOPHY
OF THE SCIENCE OF MIND AND BEHAVIOR
The fragmentation of psychology by an explosion of theoretical views, empirical techniques, and professional divisions is at once a source of its richness, and unfortunately, its impoverishment through both sheer weight and idiosyncratic isolation (Gilgen, 1987; Heiby & Staats, 1990; Staats, 1991, Tryon, 1995). From this high-dimensional chaotic activity, there seems to be some low-dimensional well-ordered chaos emerging, with a recapturing of some of the philosophical concerns of the past along with some new sensibilities about the social consciousness of the field. Bevan (1991), in touring the onion (a Kabbalist metaphor concerning the need to plumb the chaotic nature of the universe), has commented with diffident eloquence on some of these concerns, both for the field in general, and as a personal struggle. He, like the Coles, is suggesting that a new paradigm shift (Kuhn, 1962) is underway. For Bevan it involves dynamical theory:
"When I suggest that we should look to new models, I am not prepared to say precisely what those models should be. However, I believe it essential that they should recognize both the great complexity and dynamic quality of the phenomena with which psychologists deal. They should also be representative; that is, they should allow for successful generalization to settings in which the hands-on, live phenomena that are of principal interest to us occur.
"In making these comments on models and methods I would like to call special attention to Complex Systems Theory or, as it is alternatively called, nonlinear dynamics."
I would like to further suggest that the dynamical systems' point of view contributes not only to the paradigm shift occurring in the metamodeling strategies and the philosophical foundations of our science, but also self-reflectively to an understanding of some of these basic emergent concerns about the philosophic and social-ethical issues within the sociology of our science as well (Abraham, 1996b; Abraham, Bird, Bond, Goerner, Greeley, Robertson, Mosca, Rubin, & Abraham, 1995; Robertson, 1996)
The Unification of Psychology
Leibniz (1679; Leibniz & Abraham, 1995) argued for a universal mathematical language capable of unifying science (and knowledge, religion, law, culture, etc). His vision lay largely dormant as an effective intellectual agenda until the unification of science movement of the mid twentieth century which was based on logical positivism (Neurath, 1938). The limitations of the grand theories (e.g., Köhler's Gestalt approach, 1940; Lewin's field theory, 1951; Skinner's behaviorism, 1953; see Marx, 1951), especially the grandest of all, the hypothetico-deductive ones (Hull's drive reduction theory, Estes' statistical learning theory, 1959, Kantor's interbehavioral psychology, 1958) rendered them incapable of adjustment to the plethora of liberalizing and divergent findings evolving in the 60's and 70's (Maslow, 1968; Miller, 1969; Tapp, 1977; Walsh, 1992; Wilbur et al., 1986).
The social consciousness of Lewin's action research programs and SPSSI remained largely tied to traditional values and approaches of the field (Heims, 1991). Traditional analytic modeling strategies were helpful, but progress remained slow in this social arena. The passionate committment to social justice led many psychologists to cast off some of the traditional foundations and methods of the past, as they strove to study ways of changing the world, especially with respect to infringement of human rights and potential on the basis of class, race, gender, poverty, disability, etc. While at first these concerns over social justice seemed to further the increase in fractal dimensionality of the field, they now, like the dynamical systems' point of view to which they have a great kinship (Murphy & Abraham, 1995), have spawned new approaches to our science that will prove of inestimable value in the metamodeling paradigm shift (Crawford & Maracek, 1989; Mednick, 1989) and in the unification of psychology. Most germane, Crawford and Maracek (1989) state:
"The [traditional] experimental paradigm has also been criticized for emphasizing discovery of universal (and static) laws of behavior. If one holds truth to be historically and culturally situated, then methods should focus on dynamic processes and regard historical and cultural influences not as `nuisance variance' but as legitimate objects of study (Hoffnung, 1985)."
"Some feminists have called for a revision of the research paradigm to one of mutual collaboration, in which the research participant is acknowledged as the primary interpreter of her or his experience and the research initiator is acknowledged as emotionally involved and as changed by the process of doing the research.
". . . the conception of gender as a process cannot be readily accommodated within conventional methods of psychological research. When social organization and social relations are the subjects of inquiry, laboratory experiments are not necessarily the best means of study. Laboratory methods are designed to `decontextualize' the variables under study, that is, to isolate them from the contaminating influences of ongoing `real-life' processes. But gender is constructed and reconstructed through precisely these processes.
"Yet psychology does have a rich tradition of inquiry outside the positivist model of laboratory manipulation of isolated variables: field research, observational techniques, content analysis of open-ended responses, participant-observation, and case studies are a few examples."
These insights are raised not to show that feminist psychology, like developmental psychology, highlights the relevance of the dynamical systems' point of view with which they are syntonic, but that the very subject matter for study forces a self-organizational, self-reflective paradigm shift on the field of psychology which should have unifying effects that transcend any particular subject matter.
The dynamical systems' point of view contributes to the unification of psychology in two ways. The first is in providing a language that is based on a mathematical approach that is both relatively competent to deal with the complexity of interactive change and yet relatively easily to communicate, especially in the visual geometric version now fairly readily produced by computer simulation. Leibniz is thus brought up to date on two scores. His general characteristic is the unified language feature; his calculus, now evolved to dynamics, provides the methodological foundation. A good start to answering Gosling's (1986) plea for a coherent epistemic structure is provided by the dynamical systems' point of view.
The second relevance of the dynamical systems' point of view is to put the balance between the benefits of diversity and unification into perspective. Psychology may be considered as a chaotic attractor with convergent and divergent tendencies. There are self-organizational tendencies in psychology to rebalance these when one tends to dominate the other. As Staats (1991) says in recognition of the need for balance,
"The value of unification activities for the science, relative to proliferation activities, depends on where the science is on the disunity-unity dimension of development."
Rychlak (1981) has also stressed the importance of dialectic tension among disparate views, including their contriubiton to the evolution of unification. The unification potential of the dynamical systems' point of view as a metamodeling strategy, as an evaluation of the nature of the subject, mind, for study, and as a universal language for psychology, will not imply a hegemony of ideas, but mainly provide a forum for the evolution to a better balance between unity and diversity. Common features may more easily emerge, uniquely useful variables will contribute with greater ease to the diverse webb of interrelated phenomena comprising our field. The benefits of communication were stressed also by Staats:
"It should be emphasized that the ability to see commonality, in principle, through thickets of superficial difference is at the heart of creating unified science"
The dynamical systems' point of view participates in, and reflexively comments on the evolution of psychology. It should contribute to unified positivism and its gylanic, cooperative effort.
Determinism and Free Will
There are two senses in which the dynamical systems' point of view can contribute to the dialogue in psychology concerning determinism and free will. One is in providing a framework or model for choice behavior. The other is to highlight the unprovability of determinism or intererminism. The former must refer back to the Newtonian/Bergsonian distinction concerning time and awarness in mind. The vectorfield that generates a portrait acts at each moment over a succession of moments as linear time progresses. In this sense, it is not teleological. Of course, when that vectorfield exists in a mind, that mind is capable of constructing that field, and in having goals, imagined future views of the field, and viewing the portrait itself. It becomes Bergsonian, and can construct a map not only of visited portions of the response diagram, but of imaginary and novel ones. The integration (and novel extrapolation) of time over attractors and response diagrams provides a teloponsive utilization of them (Lewin, 1951; Loye, 1983; Loye & Eisler, 1987; Rychlak, 1981, 1991); it empowers a self-organizational control. Where you want to go, what attractors you wish to choose, and how to get there, are provided by your vision of the future behavior of the system. Freedom of choice is conceived as movement in the control space, or by restarting initial conditions to select a trajectory in the proper basin leading to the desired attractor. As Kugler et al. (1990) put it:
"A system with the ability to make choices must have the capacity for intending and not just for perceiving and moving. . . We identify intention with an operator that selects, from among all possible final states of a system, a specific final state to be the goal. Goal selection, we shall argue, is the sensitivity of a self-organizing system to nonlocal constraints that have determinate local effects — such as breaking ties between competing attractors." [Includes movement in the control space enabled by the MIND event-time view of the response and network diagram of complex dynamical systems and schemes.]
"A system intends a particular final condition (goal) if from among the possible initial conditions it selects the one that
permits attainment of the specified final condition . . . [and thus is] capable of true choice behavior." [Choice of initial conditions also requires the cognitive map of dynamical schemes.]
While this may place freedom of choice under some of the constraints (any model and metamodeling paradigm places constraints while simultaneously liberating and liberalizing) of the dynamical systems' point of view, there is thus indeed support for the idea of free will. It should be clear that this position is not an inevitable result, as the dynamical view could be left in an operational level of analysis, and explain such behavior in the usual behavioral fashion, with or without strict causality additionally imposed (operationism is not causal). Nonetheless, free will is a natural extension of the dynamical view. From the viewpoint of neurological positivism of free choice being generated by a dynamic mind, it can not be said with certainty whether this view falls more within the context of Sappington's (1990) soft determinism or libertariansism but it meets his libertarian requirement that concepts of a uniquely human free will be capable of being operationalized and contribute to better prediction and control. This position also could be viewed as transcending these requirements. The inability to resolve the soft versus libertarian evaluation, returns us to considerations of linear time, and principles of indeterminism within dynamical systems' theory itself, and how they relate to issues of determinism generally.
The deterministic models of differential calculus assume infinite resolution and duration in time and space. The limits to our observation of the real world, by personal and experimental means, do not have such resolution or duration. A choice between determinism and free will, whether at a quantum or a psychological level, is, therefore, relegated to be unresolvable, in the Gödelian sense of a proposition whose truth or falsity is unprovable. Or according to Poincaré:
"It can only be said: If such and such conditions are realized, it is probable that such a phenomenon will occur, very nearly." (Poincaré, 1905)
Sounds familiar to a positivist? Wait, try this:
"When slight differences in the causes produce vast differences in the effects, why are these effects distributed according to the laws of chance?
"This curve [trajectory], understand, may remain continuous in the analytic sense of the word...But practically it will not be continuous..It would become impossible to trace the curve with a pencil [comment: he means an infinitely sharp one]. We may in all confidence assume its continuity." (Poincaré, 1908.)
He was thus a determinist. But such a choice as that is a matter of faith that must be made outside the real system, and which must be made in the pragmatic Jamesian sense. From the chaos view and from the insensitivity to initial conditions just alluded to by Poincaré, indeterminism means your never know precisely where your are in the chaotic attractor, and therefore can't predict exactly the outcomes of your choices.
Furthermore, this indeterminism exists at every point as you travel along a trajectory. When should you remain on a trajectory or jump to another? What departure do you make from a saddle point? But you are confronted by choices, including the open ended one of trying to make your life more meaningful. You can bifurcate to portraits providing more fulfilling attractors and choose a path to get you there. These choices are real, given your imperfect knowledge state. You really posses the ignorance. You really make a choice. That the actual reality may be determinate or indeterminate is in the well known realm of badly posed questions. It is irrelevant!
While we point with enthusiasm at the revolution that chaos theory is providing to get us to search for information among what previously was discarded by error terms, newer versions of chaos theory often inject noise into the models. As always with the recognition or introduction of noise, this use of noise could be a confession of ignorance, or an affirmation of a fundamental principle of how nature operates (as asserted by quantum theory). We have seen that the divergent features are as important to the functioning of a chaotic system as are the attractive ones, and are especially important for people in constructing alternative models of their future.
The Humanist Mission
Psychology has two basic missions. One is the better understanding of human nature. The second is the nurturing of that nature to fulfill its potential. This is the humanist mission. This mission does not stop with a concern for individuals learning to develop more fully. It implies that a concern for others is itself an attribute that should be fostered. Our mission is first to be more sensitive to the human enterprise we study, to be compassionate about people (Combs, 1992). By example, and by considering such sensitivity, compassion, and empathy as goal themselves, these characteristics could become a part of everybody's self-fulfillment. I think that the dynamical view contributes to this mission, by emphasizing the interconnectedness of individuals and the self-organization within those interconnected networks, by seeing the long term features of the lives of individuals and of societies, and thus, by increasing an awareness of the future, and the need to plan for it for the good of self and society.
More concretely, it contributes to the ability of the science to join its subject, human nature, to its complex contextual reality. Danziger (1985), in reviewing the history and sociology of psychological experiment, observed the inadequacy of traditional research in this effort. He said,
"A more promising approach would involve raising questions about relationships between the social structure of knowledge-generating situations and the nature of their products."
The dynamical view enables an exploration of those relationships.
Summary Three
(1) The dynamical view can contribute to the evolution of a better balance between unity and diversity in psychology. (2) The dynamical view is both determinist and indeterminate; it empowers free-will. (3) The dynamical view contributes to the empowerment of the humanist mission in psychology, through a more realistic characterization of complexity, longitudinal forecasting, and compassion for individuals in their interconnectedness.
EPILOGUE
Neurological positivism and ecological physics are holistic views of phenomenology, brain, behavior, and environment (herein called mind). They are naturally synergistic with the dynamical systems' view of the universe and its metamodeling strategy. Processes of the mind can be represented as complex dynamical systems and their portraits containing attractors, fixed point, periodic, and especially chaotic. Functionally meaningful attractors require integration over time by the mind's eye, and 'insensitivity to initial conditions' highlights the ability of an attractor of the mind to be realized and represented by more than a single trajectory, a sort of generalization or equivalence of trajectories and invariant properties of the dynamical system. Awareness relates to the magnitude and stability of attractors of the mind, and bifurcations between them occur continually, on cognitive, ontogenetic. and phyologenetic time scales. A chairos-durée temporal cognitive map of the dynamical scheme enables its navigation including charting novel courses of intentional behavior. The self-control of bifurcations empowers self-organization of selves and societies to become more interesting, complex, fulfilling, and compassionate. A better balance of unification and diversity in psychology and a recognition of the free-will nature of mind can be clarified by the dynamical view. It is a privilege and responsibility of the dynamical systems' theoretical point of view to contribute to the humanistic mission of psychology as well as its scientific mission. Psychology is in the midst of a healthy self-reorganizational effort.
REFERENCES
Abraham, F. D. (1995). Dynamics, bifurcation, self-organization, chaos, mind, conflict, insensitivity to initial conditions, time, unification, diversity, free-will, & social responsibility. In R. Robertson & A. Combs (Eds.), Chaos Theory in Psychology and the Life Sciences. Hillsdale NJ USA: Erlbaum.
Abraham, F. D. (1996a). The dynamics of creativity & the courage to be. In W. Sulis & A. Combs (Eds.), Nonlinear dynamics in human behavior. Studies of nonlinear phenomena in life science, vol. 5. Singapore: World Scientific.
Abraham, F. D. (1996b) The Berezin-Protagoras-Abraham Correspondence: A reply to Robertson & Berezin. Dialogue, 1. http://www.pacweb.com/blueberry/
Abraham, F. D. (1997). Nonlinear coherence in multivariate research: Invariants and the reconstruction of attractors. Nonlinear Dynamics, Psychology, and Life Sciences, 1, 7-.
Abraham, F. D., Abraham, R. H., and Shaw, C. D. (1990). A visual introduction to dynamical systems theory for psychology. Santa Cruz: Aerial.
Abraham, F. D., Bird, R., Bond, R., Goerner, S., Greeley, L, Robertson, R., Mosca, F., Rubin, S., & Abraham, F. (1995). Xaos at the Xrossroads: A virtual Panel Discussion. http://www.pacweb.com/blueberry/
Abraham, F. D., Bryant, H., Mettler, M., Bergerson, W., Moore, F., Maderdrut, J., Gardiner, M., Walter, D., & Jennrich, R. (1973). Brain Reserch, 49, 349-366.
Abraham, F. D. & Gilgen, A. R. (Eds.). (1995). Chaos Theory in Psychology. Westport CN USA: Greenwood.
Abraham, R. H. (1994). Chaos, gaia, eros. San Francisco: Harper and Row.
Anderson, C. M., & Mandell, A. J. (1996). Fractal time and the foundations of consciousness: Vertical convergeence of 1/f phenomena from ion channels to behavioral states. In E. MacCormac & M. I. Stamenov (Eds.), Fractals of brain, fractals of mind. Amsterdam: John Benjamins.
Barnsley, M. F. (1988). Fractal modelling of real world images. In H. -O. Peitgen and D. Saupe (Eds.), The science of fractal images. New York: Spinger-Verlag.
Bevan, W. (1991). A tour inside the onion. American Psychologist, 46, 475-483.
Bressler, S. L., Coppola, R., & Nakamura, R. (1993). Eposodic multiregional cortical coherence at multiple frequencies during visuaul task performance. Nature, 366, 153-156.
Burlingame, G. M., Fuhriman, A., & Barnum, K. (1995). Group therapy as a nonlinear dynamical system: Analysis of therapeutic communication for chaotic patterns. In F. D. Abraham & A. R. Gilgen (Eds.), Chaos Theory in Psychology. Westport CN USA: Greenwood.
Bütz, M. (1992). The fractal nature of the development of the self. Psychological Reports, 71, 1043-1063.
Cairns, R. B. (1990). Towards a developmental science. Psychological Science, 1, 42-44.
Cole, M. and Cole, S. R. (1989). The development of children. New York: Freeman.
Combs, A. 1992. Cooperation. Philadelphia et al.: Gordon & Breach.
Combs. A. (1995). Psychology, chaos, and the process nature of consciousness. In F. D. Abraham & A. R. Gilgen (Eds.), Chaos Theory in Psychology. Westport CN USA: Greenwood.
Conforti, M. (1994). Morphogenetic dynamics in the analytic relationship. Psychological Perspectives, 30(Fall/Winter), 12-21.
Crawford, M., and Maracek, J. (1989). Psychology reconstructs the female. Psychology of Women Quarterly, 13, 147-165.
Danziger, K. (1985). The origins of the psychological experiment as a social institution. American Psychologist, 40, 133-140.
Deux, K., and Major, B. (1987). Putting gender into context: An interactive model of gender-related behavior. Psychological Review, 94, 369-389.
Elka‹m, M., Goldbeter, A., and Goldbeter-Merinfeld, E. (1987). Analysis of the dynamics of a family system in terms of bifurcations. Journal of Social and Biological Structures, 10, 21-36.
Estes, W. K. (1959). The statistical approach to learning theory. In S. Koch (Ed.), Psychology: A study of a science. Vol. 2. General systematic formulations, learning, and special processes. New York: McGraw-Hill.
Fogel, A. (1988). Dynamic systems in human development: the inhibition of attention to mother in early infancy. In J.A.S. Kelso, A. J. Mandell, and M. F. Shlesinger (Eds.), Dynamic patterns in complex systems. Singapore: World Scientific.
Freeman, W. J. (1990). Nonlinear neural dynamics in olfaction as a model for cognition. In E. Basar (Ed.), Chaos in Brain Function. Berlin/Heidelberg: Springer-Verlag.
Gampel, D. H. (1991). Fractal selves, the fragility of relationships, and chaos theory. Paper presented at the Inaugural Conference for the Society for Chaos Theory in Psychology, San Francisco.
Gibson, J. J. (1979). The ecological approach to visual perception. Boston: Houghton-Mifflin.
Gilgen, A. R. (1987). The psychological level of organization in nature and interdependencies among major psychological concepts. In A. W. Staats and L. P. Mos (Eds.), Annals of theoreticcal psychology (Vol. 5). New York: Plenum.
Goerner, S. J. (1994). Chaos and the evolving ecological universe: A study in the science and human implications of a new world hypothesis. New York: Gordon & Breach.
Gosling, J. (1986). Analysis and strategy in the search for unity: Epistemic principles for psychology. International Newsletter of Uninomic Psychology, 2, 13-19.
Hanlon, H. (1996). Topographically Different regional networks impose structural limitations on both sexes in early postnatal
development in K. H. Pribram & J. King (Eds.), Learning as self-organization. Mahwah: Lawrence Erlbaum. "
Heiby, E. M., and Staats, A. W. (1990). Depression and its classification. In G. Eifert and I. Evans (Eds.), Unifying behavior therapy. New York: Springer.
Heims, S. J. (1991). The cybernetics group. Cambridge: MIT.
Hoffnung, M. (1985). Feminist transformation: Teaching experimental psychology. Feminist Teacher, 2, 31-35.
Hull, C. L. (1943). Principles of behavior. New York: Appleton.
James, W. (1890/1952). Principles of psychology(2 Vols.). New York: Holt. Reprinted, Chicago: Encyclopaedeia Britinnica.
Kantor, J. R. (1958). Interbehavioral psychology. Bloomington IN USA: Principia.
Killeen, P. R. (1992). Mechanics of the animate. Journal of the Experimental Analysis of Behavior, 57, 429-463.
Köhler, W. (1940). Dynamics in psychology. New York: Liveright.
Kohonen, T. (1972). Correlation matrix memories. IEEE Transactions: Computers, 21, 353-359.
Kohonen, T. (1977). Associative memory: A system theoretic approach. Berlin: Springer-Verlag.
Kohonen, T. and Oja, E. (1987). Technical comments. Science, 235, 1227.
Kugler, P. N., Shaw, R. E., Vincente, K. J., & Kinsella-Shaw, J. (1990). Inquiry into intentional systems I: Issues in ecological physics. Psychological Research, 52, 98-121.
Kuhn, T. S. (1962/1970). The structure of scientific revolutions (2nd ed.). Chicago: University of Chicago.
Langs, R., and Badalamenti, A. (1991). Toward a science of the mind. The Social Dynamicist, 2 (3), 1-3.
Leibniz, G. W. F. von (1679/1969). On the general characteristic. In L. E. Loemmker, (Ed. and trans.), Gottfried Wilhelm Leibniz: Philosophical papers and letters. Dordrecht/Boston: Reidel.
Liebniz, G. W. F., & Abraham, F. D. (1666-1695; 1995). The Leibniz-Abraham correspondence. In Abraham, F. D. & Gilgen, A. R. (Eds.), Chaos Theory in Psychology. Westport: Greenwood/Praeger.
Levan, S. (1992). Learned helplessness, memory, and the dynamics of hope. In In D. S. Levine & S. J. Leven (Eds.), Motivation, emotion, and goal direction in neural networks. Hillsdale NJ USA: Erlbaum.
Levine, D. S., Leven, S. J., & Prueitt, P. S. (1992). Integration, disintegfration, and the frontal lobes. in D. S. Levine & S. J. Leven (Eds.), Motivation, emotion, and goal direction in neural networks. Hillsdale NJ USA: Erlbaum.
Lewin, K. (1951). Field theory in social science. New York: Harper & Row.
Lorenz, E. N. (1963). Deterministic nonperiodic flow. Journal of the Atmospheric Sciences, 20, 130-141.
Loye, D. (1983). The sphinx and the rainbow: Brain, mind and future vision. Boulder: Shambala.
Loye, D., and Eisler, R. (1987). Chaos and transformation: Implications of nonequilibrium theory for social science and society. Behavioral science, 32, 53-65.
Maas, J. P. (1988). Is psychology like Little Jack Horner, or does systems theory have something to offer us? Paper presented at the XXIV International congress of Psychology, Sydney, Australia.
Macy. J. (1991). Mutual causality in Buddhism and general systems theory: The dharma of natural systems. Albany NY USA: State University of New York.
Magdamo, P. (unpublished notes, and concert presentations). Palaas and Salarung: A folktale of self-referential justice of the Philippine Monobo.
Mandell, A. J. (1980). Toward a psychobiology of transcendence: God in the brain. In R. J. Davidson and J. M. Davidson (Eds.), The psychobiology of consciousness. New York: Plenum.
Marx, M.H. (Ed.). (1951). Psychological theory. New York: Macmillan.
Maslow, A. (1968). Toward a psychology of being. Princeton: Princeton.
May, J. (alias Goerner, S.), and Groder, M. (1989). Jungian thought and dynamical systems. Psychological Perspectives, 20, 142-155.
Masling, J. M., Bornstein, R. F., Poynton, F. G., Reed, S., and Katkin, E. S. (1991). Perception without awareness and electrodermal responding: A strong test of subliminal psychodynamic activation effects. Journal of Mind and Behavior, 12, 33-47.
Maturana, H. R. (1969). The neurophysiology of cognition. In P. Garvin (Ed.), Cognition: A multiple view. New York: Spartan.
Mednick, M.T. (1989). On the politics of psychological constructs. American Psychologist, 44, 1118-1123.
Miller, N. E. (1959). Liberalization of basic s-r concepts: extensions to conflict behavior, motivation, and social learning. In S. Koch (Ed.), Psycholgy: A study of a science. Vol. 2. General systematic formulations, learning, and special processes. New York: McGraw-Hill.
Mosca, F. (1995). In F. D. Abraham & A. R. Gilgen (Eds.), Chaos Theory in Psychology. Westport CN USA: Greenwood.
Mpitsos, G.J. (1989). Chaos in brain function and the problem of nonstationarity: A commentary. In E. Basar and T.H. Bullock (Eds.), Brain dynamics. Berlin: Springer-Verlag.
Murphy, P. L. (1995). Feminist psychology: Prototype of the feminist revolution in psychology. In F. D. Abraham & A. R. Gilgen (Eds.), Chaos theory in psychology. Westport: Greenwood/Praeger.
Natsoulas, T. (1991). Consciousness and commissurotomy: III. Toward the improvement of alternative conceptions. Journal of Mind and Behavior, 12, 1-32.
Neurath, O. (1938). Unified science as encyclopedic integration. In O. Neurath, R. Carnap, and C. Morris (Eds.), International encyclopedia of unified science (Vol. 1). Chicago: University of Chicago.
Orme-Johnson, D. W., and Haynes, C. T. (1981). EEG phase coherence, pure consciousness, creativity, and TM-Sidhi experiences. International Journal of Neuroscience, 13, 211-217.
Paar, D. W. (1992). Introducing confusion to create change. The Psychotherapy Patient, 8, 93-102.
Poincaré, H. (1899). Les méthodes nouvelles de la mécanique céleste, Vols. 1-3. Paris: Gauthier-Villars.
Poincaré, H. (1905/1913/1958). Valeur de science. Paris, Flammarion. The value of science, G.B. Halstead (trans., 1913). New York: Science Press. Reissued 1958, New York: Dover.)
Poincaré, H. (1908). Science et Méthode. Paris: Flammarion. Science and method. G. B. Halstead (trans., 1913), New York: Science Press. Reissued New York: Dover. And, F. Maitland (trans., 1914). London, and reissued later, New York: Dover. From the chapter "Chance", which is also reprinted in J.R. Newman (Ed.). The world of mathematics, Vol 2. New York: Simon and Schuster.
Pribram, K. H. (1991). Brain and perception: Holonomy and structure in figural processing. Hillsdale NJ USA: Erlbaum.
Prigogine, I. and Stengers, I. (1984). Order out of chaos. New York: Bantam.
Raphaely, D. (1989). Intimations of chaos: Applying chaos theory to analyzing interpersonal process. Paper presented at the American Psychological Association convention, New Orleans.
Reidbord S. P., & Redington, D. J. (1992). Psychophysiological processes during insight-oriented therapy: further investigations into nonlinear psychodynamics. The Journal of Nervous and Mental Diseases, 180, 649-657.
Rindfuss, R. R., Swicegood, C. G., Rosenfeld, R.A. Disorder in the life course: How common and does it matter? American Sociological Review, 52, 785-801.
Robertson, R. (1989). The evolution of number. Psychological Perspectives, 20, 128-141.
Robertson, R. (1996). A Sense of Wonder. Paper presented at the 6th Annual Conference of the Society for Chaos Theory in Psychology and the Life Sciences, Berkeley. http://www.pacweb.com/blueberry/
Rossi, E. L. (1989). Archetypes as strange attractors. Psychological Perspectives, 20, 4-14.
Rychlak, J. F. (1981). A philosophy of science for personality theory (2nd ed). New York: New York University Press.
Rychlak, J. F. (1991). Some theoretical and methodological questions concerning Harcum's proposed resolution of the free will issue. The Journal of Mind and Behavior, 12, 135-150.
Sabelli, H. (1990). Personalization, a new vision beyond individualism and socialism. In H. sabelli and J. Synnestvedt, (Eds.), Personalization: A new vision for the millennium. Chicago: Society for the Advancement of Clinical Philosophy.
Sappington, A. A. (1990). Recent psychological approaches to the free will versus determinism issue. Psychological Bulletin, 108, 19-29.
Schwalbe, M.L. (1991). The autogenesis of the self. Journal for the Theory of Social Behavior, 21, 269-295.
Skinner, B. F. (1953) Science and human behavior. New York: Macmillan.
Skinner, J. E., Martin, J. L., Landisman, C. E., Mommer, M. M., Fulton, K., Mitra, M., Burton, W. D., and Saltzberg, B. (1990). Chaotic attractors in a model of neocortex: Dimensionalities of olfactory bulb surface potentials. In E. Basar (Ed.), Chaos in Brain Function. Berlin/Heidelberg: Springer-Verlag.
Smith, L. B (1995). Stability and variability: the geometry of children's novel word interpretations. In F. D. Abraham & A. R. Gilgen (Eds.), Chaos Theory in psychology. Westport CN USA: Greenwood.
Staats, A. W. (1991). Unified positivism and unification psychology. American Psychologist, 46, 899-912.
Stoffregen, T. A., Schmuckler, M. A., and Gibson, E. J. (1987). Use of central and peripheral optical flow in stance and locomotion in young walkers. Perception, 16, 113-119.
Swinney, F. (1991). Chaos consciousness in psychotherapy. Paper presented at the Inaugural Conference for the Society for Chaos Theory in Psychology, San Francisco.
Tapp, J. T. (1969). Reinforcement and behavior. New York/London: Academic.
Thelen, E. (1988). Dynamical approaches to the development of behavior. In J.A.S. Kelso, A.J. Mandell, and M.F. Shlesinger (Eds.), Dynamic patterns in complex systems. Singapore: World Scientific.
Tryon, W. W. (1995). Synthesizing psychological schisms through connectionism. In Abraham, F. D. & Gilgen, A. R. (Eds.), Chaos Theory in Psychology. Westport CN USA: Greenwood.
Vandervert, L.R. (1993). Neurological Positivism's evolution of mathematics. The Journal of Mind and Behavior, 14, 277-288.
Varela, F. (1979). Principles of biological autonomy. New York: Elsevier/North-Holland.
Voeks, V. W. (1954). Gradual strengthening of s-r connections or increasing number of s-r connections. Journal of Psychology, 39, 289-299.
Walsh, R. (1992). Transpersonal psychology synthesis. Journal of Humanistic Psychology, 32, 19-45.
Weiner, N. (1948). Cybernetics or control and communication in the animal and the machine. New York/Paris: Wiley.
Wilber, K, Engler, J., and Brown, D. (Eds.). (1986). Transformations of consciousness: Conventional and contemplative perspectives on development. Boston: New Science Library/Shambala.
Created: 10/21/96 Updated: 11/13/96

